回溯算法

回溯算法的经典问题

回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

回溯算法的统一解题模板

确定回溯函数模板返回值以及参数
1

void backtracking(参数)
- 回溯算法中函数返回值一般为void。结果集合使用全局变量
- 回溯算法需要的参数所以一般是先写逻辑，然后需要什么参数，就填什么参数。
确定回溯算法的终止条件
1 2 3 4

if (终止条件) { 存放结果; return; }
- 一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

确定单次遍历过程

1
2
3
4
5


for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

处理节点
递归处理
回溯
- 对于引用数据类型必须要回溯
- 对于基本数据类型如果在for循环内进行修改则需要回溯，因为递归返回后这个值是不会自动回滚，和递归前的值不一致
- 对于基本数据类型如果作为参数传入递归函数中则不需要回溯，因为每次递归调用使用的 sum 都是独立的，不影响上一层递归。

组合问题

统一解题模板

确定回溯函数模板返回值以及参数
1

void backtracking(int startIndex,题目参数)
- 回溯算法中函数返回值一般为void。结果集合使用全局变量
- 回溯算法需要的参数中需要一个startIndex，记录记录本层递归的中，集合从哪里开始遍历
确定回溯算法的终止条件
1 2 3 4

if (终止条件) { 存放结果; return; }
- 通常搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。
确定单次遍历过程
1 2 3 4 5

for (int i=startIndex;i<nums.length;i++) { 处理节点; backtracking(i+1,选择列表); // 递归回溯，撤销处理结果 }
- 处理节点
  - 去重逻辑
    - 先创建一个used数组作为全局变量
    - 树层去重
      - 利用used数组去重：先对数组排序，used[i - 1] == false，说明同一树层candidates[i - 1]使用过
      - 利用set去重：先对数组排序，在for循环外创建一个set，用set检验是否使用过
    - 树枝去重：used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
- 递归处理
- 回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void backtracking(题目参数,int startIndex){
	if (终止条件) {
    	存放结果;
    	return;
	}
    // 在这里建立set集合进行树层去重
    for (int i=startIndex;i<nums.length;i++) {
    	处理节点;
   		backtracking(路径，选择列表); // 递归
    	回溯，撤销处理结果
	}
}

77.组合2

leetcode 77 组合

题目描述

力扣题目链接(opens new window)

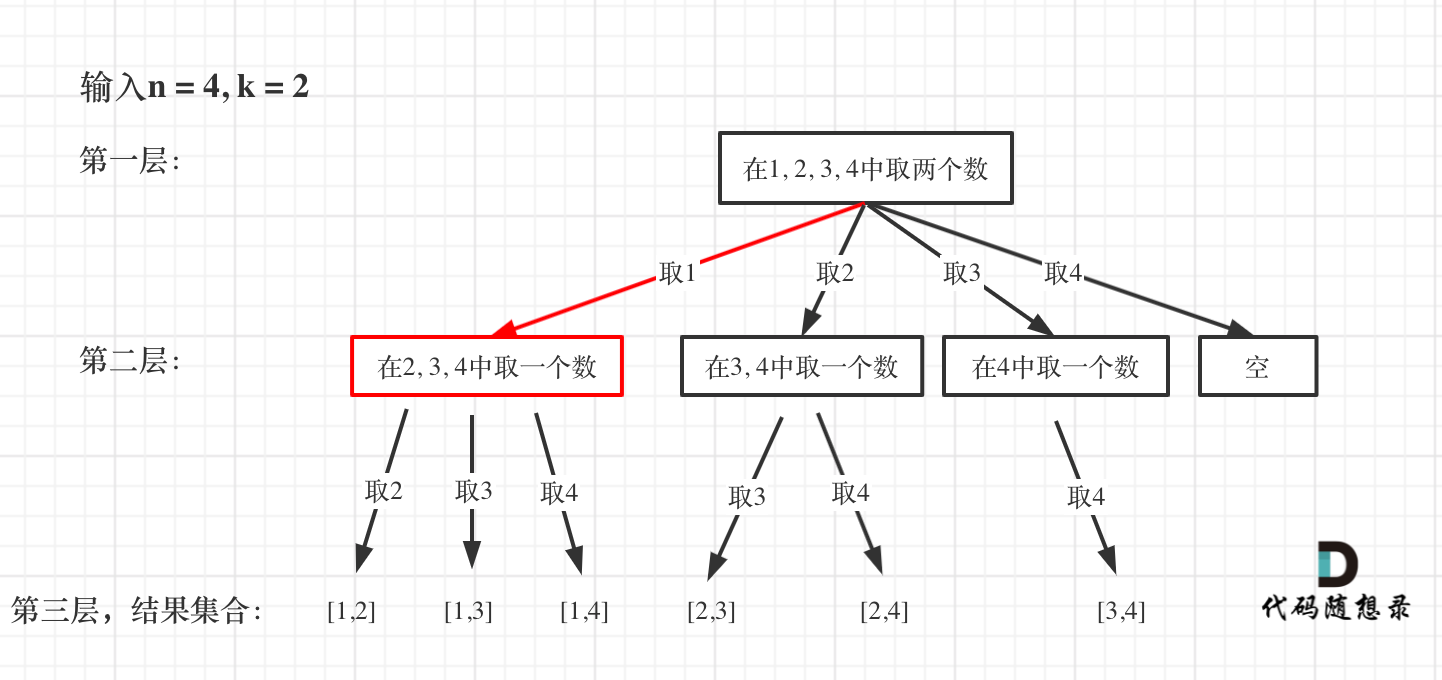
给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

思路解析

确定回溯函数模板返回值以及参数
- 返回值为 void
- 参数为n，k，startIndex（记录下一层递归，搜索的起始位置）
确定回溯算法的终止条件
- 当path的大小为k时，将path加入res
确定单次遍历过程
- 遍历1…n
  - 将数字i加入路径中
  - 递归处理i+1
  - 回溯处理数字i，将i从path中移除
遍历过程中可以进行剪枝处理
- 已经选择的元素个数：path.size();
- 还需要的元素个数为: k - path.size();
- 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution {
    List<List<Integer>>res;
    List<Integer>path;
    public List<List<Integer>> combine(int n, int k) {
        res=new ArrayList<>();
        path=new ArrayList<>();
        backtracking(n,k,1);
        return res;
    }

    public void backtracking(int n,int k,int startIndex)
    {
        // 终止条件
        if(path.size()==k)
        {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=startIndex;i<=n-(k-path.size())+1;i++)
        {
            path.add(i);
            backtracking(n,k,i+1);
            path.remove(path.size()-1);
        }
    }
}

leetcode 216 组合总和III

题目描述

力扣题目链接(opens new window)

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且 每种组合中不存在重复的数字 。

说明：

所有数字都是正整数。
解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

思路解析

确定回溯函数模板返回值以及参数
- 返回值为 void
- 参数为n，k，startIndex（记录下一层递归，搜索的起始位置）
确定回溯算法的终止条件
- 当path的大小为k时判断是否sum==n
确定单次遍历过程
- 遍历1…9
  - 处理数字i
    - 将数字i加入路径中
    - sum+=i
  - 递归处理i+1
  - 回溯处理数字i
    - 将i从path中移除
    - sum-=i
遍历过程中可以进行剪枝处理
- 已经选择的元素个数：path.size();
- 还需要的元素个数为: k - path.size();
- 在集合n中至多要从该起始位置 : 9 - (k - path.size()) + 1，开始遍历

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class Solution {
    List<List<Integer>>res;
    List<Integer>path;
    public List<List<Integer>> combinationSum3(int k, int n) {
        res=new ArrayList<>();
        path=new ArrayList<>();
        backtracking(k,n,1,0);
        return res;
    }

    public void backtracking(int k,int n,int startIndex,int sum)
    {
        // 终止条件
        if(path.size()==k)
        {
            if(sum==n)
                res.add(new ArrayList<>(path));
            return;
        }
        // 单次遍历
        for(int i=startIndex;i<=9-(k-path.size())+1;i++)
        {
            sum+=i;
            path.add(i);
            backtracking(k,n,i+1,sum);
            path.remove(path.size()-1);
            sum-=i;
        }
    }
}

leetcode 17 电话号码的数字组合

题目描述

力扣题目链接(opens new window)

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

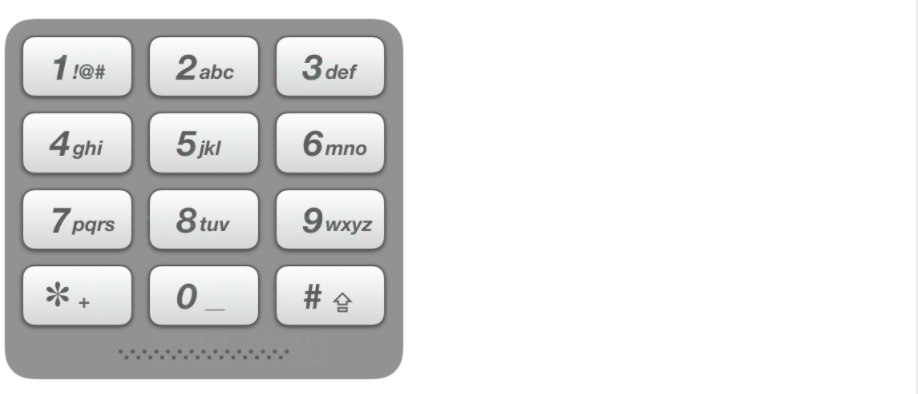
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

17.电话号码的字母组合

示例:

输入：“23”
输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

思路解析

建立数字和字母的映射关系
确定回溯函数模板返回值以及参数
- 返回值为 void
- 参数为index（记录选择遍历的第几个字母）
确定回溯算法的终止条件
- 当遍历的数字下标等于字符串长度，将局部字符串加入结果
确定单次遍历过程
- 获取遍历到的数字对应的字符串
- 遍历字符串的每个字符
  - 将字符加入局部字符串
  - 递归处理index+1
  - 回溯处理

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
    List<String>res=new ArrayList<>();
    StringBuffer temp=new StringBuffer();
    String[]map=new String[]{" "," ","abc","def","ghi","jkl","mno",
    "pqrs","tuv","wxyz"};
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return res;
        }
        backtrack(digits,0);
        return res;
    }

    public void backtrack(String digits,int index)
    {
        // 终止条件
        if(index==digits.length())
        {
            res.add(temp.toString());
            return;
        }
        //单次递归
        char ch=digits.charAt(index);
        String str=map[ch-'0'];
        for(int i=0;i<str.length();i++)
        {
            temp.append(str.charAt(i));
            backtrack(digits,index+1);
            temp.deleteCharAt(temp.length()-1);
        }

    }
}

leetcode 39 组合总和

题目描述

力扣题目链接(opens new window)

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为： [ [7], [2,2,3] ]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

思路解析

先对数组进行排序
确定回溯函数模板返回值以及参数
- 返回值为 void
- 参数为candidates，sum，target，startIndex（记录下一层递归，搜索的起始位置）
确定回溯算法的终止条件
- 当sum==target将path加入res
确定单次遍历过程
- 从startIndex开始遍历
  - 若sum+candidates[i]>target可以直接停止循环
  - 处理数字i
    - 将数字i加入路径中
    - sum+=i
  - 递归处理i
  - 回溯处理数字i
    - 将i从path中移除
    - sum-=i

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
    List<List<Integer>>res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates); // 先进行排序
        backtrack(candidates,target,0,0);
        return res;
    }

    public void backtrack(int[]candidates,int target,int startIndex,int sum)
    {
        if(sum==target)
        {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=startIndex;i<candidates.length;i++)
        {
            if(sum+candidates[i]>target)
                break;
            path.add(candidates[i]);
            sum+=candidates[i];
            backtrack(candidates,target,i,sum);
            sum-=candidates[i];
            path.removeLast();
        }
    }
}

leetcode 40 组合总和II

题目描述

力扣题目链接(opens new window)

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:

1
2
3
4
5
6


[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:

1
2
3
4


[
  [1,2,2],
  [5]
]

思路解析

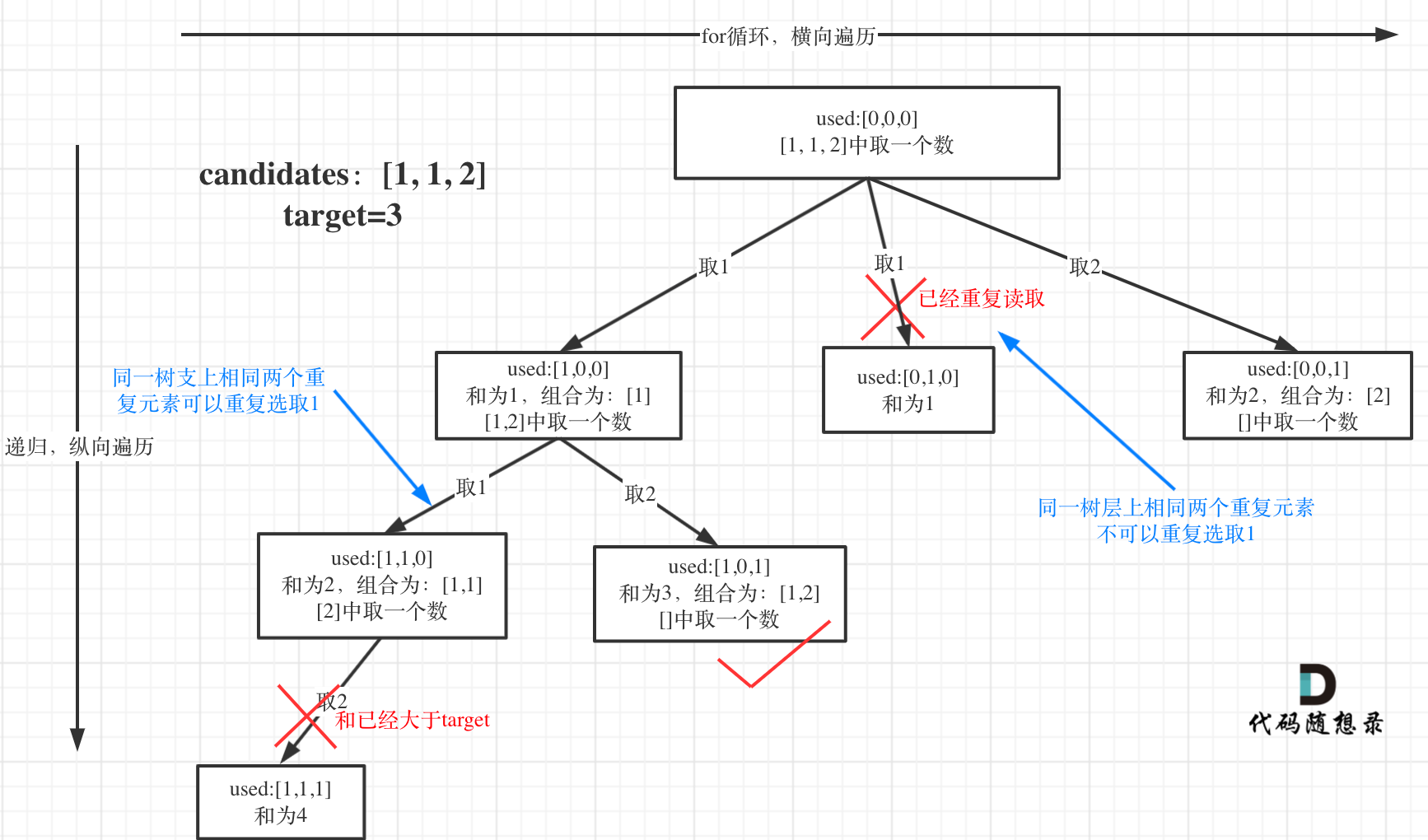
本题的重点在于如何去重，以及去重的角度。

元素在同一个组合内是可以重复的，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

40.组合总和II

先对数组进行排序
确定回溯函数模板返回值以及参数
- 返回值为 void
- 参数为candidates，sum，target，startIndex（记录下一层递归，搜索的起始位置）
确定回溯算法的终止条件
- 当sum==target将path加入res
确定单次遍历过程
- 从startIndex开始遍历
  - 若sum+candidates[i]>target可以直接停止循环
  - 若used[i - 1] == false，说明同一树层candidates[i - 1]使用过，continue之后的操作
  - 处理数字i
    - 将数字i加入路径中
    - sum+=i
    - used[i]=true
  - 递归处理i
  - 回溯处理数字i
    - 将i从path中移除
    - sum-=i
    - used[i]=false

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72


// 使用used数组
class Solution {
    List<List<Integer>>res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        boolean[]used=new boolean[candidates.length];
        Arrays.sort(candidates);
        backtrack(candidates,target,0,0,used);
        return res;
    }

    public void backtrack(int[]candidates,int target,int sum,int startIndex,boolean[]used)
    {
        if(target==sum)
        {
            res.add(new ArrayList<>(path));
        }
        for(int i=startIndex;i<candidates.length;i++)
        {
            if (sum + candidates[i] > target) {
                break;
            }
            if(i>0&&candidates[i]==candidates[i-1]&&used[i-1]==false)
                continue;
            sum+=candidates[i];
            path.add(candidates[i]);
            used[i]=true;
            backtrack(candidates,target,sum,i+1,used);
            used[i]=false;
            path.removeLast();
            sum-=candidates[i];
        }

    }
}

// 使用set去重
class Solution {
    List<List<Integer>>res;
    List<Integer>path;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        res=new ArrayList<>();
        path=new ArrayList<>();
        Arrays.sort(candidates);
        backtrack(candidates,target,0,0);
        return res;
    }

    public void backtrack(int[]candidates,int target,int startIndex,int sum)
    {
        // 终止条件
        if(sum==target)
        {
            res.add(new ArrayList<>(path));
            return;
        }
        HashSet<Integer>set=new HashSet<>();
        for(int i=startIndex;i<candidates.length;i++)
        {
            if(sum+candidates[i]>target)
                break;
            if(set.contains(candidates[i]))
                continue;
            sum+=candidates[i];
            set.add(candidates[i]);
            path.add(candidates[i]);
            backtrack(candidates,target,i+1,sum);
            path.removeLast();
            sum-=candidates[i];
        }
    }
}

切割问题

统一解题模板

切割问题类似组合问题。

例如对于字符串abcdef：

组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…..。
切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…..。
确定回溯函数模板返回值以及参数
1

void backtracking(int startIndex,题目参数)
- 回溯算法中函数返回值一般为void。结果集合使用全局变量
- 回溯算法需要的参数中需要一个startIndex，记录记录本层递归的切割位置，切割区间为左闭右闭的区间
确定回溯算法的终止条件
1 2 3 4

if (终止条件) { 存放结果; return; }
- 通常搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

确定单次遍历过程

1
2
3
4
5


for (int i=startIndex;i<nums.length;i++) {
    处理节点;
    backtracking(i+1，选择列表); // 递归
    回溯，撤销处理结果
}

处理节点
递归处理
回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void backtracking(题目参数,int startIndex)
{
	if (终止条件) {
    	存放结果;
    	return;
	}
	for (int i=startIndex;i<nums.length;i++) {
    	处理节点;
    	backtracking(路径，选择列表); // 递归
    	回溯，撤销处理结果
	}
}

leetcode 131 分割回文串

题目描述

力扣题目链接(opens new window)

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: “aab” 输出: [ [“aa”,“b”], [“a”,“a”,“b”] ]

思路解析

总体思路

递归函数参数
- 全局变量数组path存放切割后回文的子串，二维数组result存放结果集。
- startIndex作为截取位置
递归函数终止条件
- 切割线切到了字符串最后面是本层递归的终止条件。
单次遍历
- 从startIndex开始遍历字符串
  - 截取子串[startIndex，i]作为子串
  - 验证是否为回文串若是
    - 将子串加入结果集
    - 递归处理i+1
    - 回溯

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


class Solution {
    List<List<String>>res=new ArrayList<>();
    List<String>path=new ArrayList<>();
    public List<List<String>> partition(String s) {
        backtrack(s,0);
        return res;
    }
    public boolean check(String str)
    {
        int left=0;
        int right=str.length()-1;
        while(left<=right)
        {
            if(str.charAt(left)!=str.charAt(right))
                return false;
            left++;
            right--;
        }
        return true;
    }

    public void backtrack(String s,int startIndex)
    {
        //终止条件
        if(startIndex>=s.length())
        {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=startIndex;i<s.length();i++)
        {
            String str=s.substring(startIndex,i+1);
            if(check(str))
            {
                path.add(str);
                backtrack(s,i+1);
                path.removeLast();
            }

        }
    }
}

leetcode 93 复原IP地址

题目描述

力扣题目链接(opens new window)

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

例如：“0.1.2.201” 和 “192.168.1.1” 是有效的 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是无效的 IP 地址。

示例 1：

输入：s = “25525511135”
输出：[“255.255.11.135”,“255.255.111.35”]

示例 2：

输入：s = “0000”
输出：[“0.0.0.0”]

示例 3：

输入：s = “1111”
输出：[“1.1.1.1”]

示例 4：

输入：s = “010010”
输出：[“0.10.0.10”,“0.100.1.0”]

示例 5：

输入：s = “101023”
输出：[“1.0.10.23”,“1.0.102.3”,“10.1.0.23”,“10.10.2.3”,“101.0.2.3”]

提示：

0 <= s.length <= 3000
s 仅由数字组成

思路解析

递归函数参数
- 全局变量数组path存放切割后回文的子串，二维数组result存放结果集。
- startIndex作为截取位置
- pointnum记录点的个数
递归函数终止条件
- 点的个数为3时判断剩下的部分是否合格，合格则加入结果集
单次遍历
- 从startIndex开始遍历字符串
  - 截取子串[startIndex，i]作为子串，加入逗号
  - 验证截取的子串是否为合法若合法
    - 将子串加入结果集
    - pointnum++
    - 递归处理i+2
    - 回溯

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


class Solution {
    List<String>res;
    public List<String> restoreIpAddresses(String s) {
        res=new ArrayList<>();
        StringBuilder sb=new StringBuilder(s);
        backtrack(sb,0,0);
        return res;
    }

    public void backtrack(StringBuilder s,int startIndex,int pointNum)
    {
        if(pointNum==3)
        {
            if(isValid(s.toString(),startIndex,s.length()-1))
                res.add(s.toString());
            return;
        }
        for(int i=startIndex;i<s.length();i++)
        {
            if(isValid(s.toString(),startIndex,i))
            {
                s.insert(i+1,'.');
                pointNum++;
                backtrack(s,i+2,pointNum);
                pointNum--;
                s.deleteCharAt(i+1);
            }else{
                break;
            }
        }
    }
    public boolean isValid(String s,int start,int end)
    {
        if(start>end)
            return false;
        if(s.charAt(start)=='0'&&start!=end)
            return false;
        int num=0;
        for(int i=start;i<=end;i++)
        {
            if(s.charAt(i)<'0'||s.charAt(i)>'9')
                return false;
            num=num*10+(s.charAt(i)-'0');
            if(num>255)
                return false;
        }
        return true;
    }
}

子集问题

统一解题模板

确定回溯函数模板返回值以及参数
1

void backtracking(int startIndex,参数)
- 回溯算法中函数返回值一般为void。结果集合使用全局变量
- 回溯算法的参数中需要一个startIndex，记录记录本层递归的中，集合从哪里开始遍历
确定回溯算法的终止条件
1 2 3 4

将子集加入结果集 if (终止条件) { 存放结果; }
- 收集结果写在终止条件前，因为遍历到节点就要收集
- 严格意义上子集问题不需要写递归条件

确定单次遍历过程

1
2
3
4
5


for (int i=startIndex;i<nums.length;i++) {
    处理节点;
    backtracking(i+1，其他参数); // 递归
    回溯，撤销处理结果
}

处理节点
递归处理
回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void backtracking(int startIndex,参数){
	收集子集
	if (终止条件) {
    	存放结果;
   	 	return;
	}
	for (int i=startIndex;i<nums.length;i++) {
    	处理节点;
    	backtracking(i+1，其他参数); // 递归
    	回溯，撤销处理结果
	}
}

leetcode 78 子集

题目描述

力扣题目链接(opens new window)

给定一组 不含重复元素 的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

思路解析

确定回溯函数模板返回值以及参数
1

void backtracking(int startIndex,参数)
- 回溯算法的参数中需要一个startIndex，记录记录本层递归的中，集合从哪里开始遍历
确定回溯算法的终止条件
- 收集结果写在终止条件前，因为遍历到节点就要收集
- 严格意义上子集问题不需要写终止条件

确定单次遍历过程

1
2
3
4
5


for (int i=startIndex;i<nums.length;i++) {
    处理节点;
    backtracking(i+1，其他参数); // 递归
    回溯，撤销处理结果
}

将节点加入子集中
递归处理
回溯

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution {
    List<List<Integer>>res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        backtrack(nums,0);
        return res;
    }
    public void backtrack(int[]nums,int startIndex)
    {
        res.add(new ArrayList<>(path));
        if(startIndex>=nums.length)
        {
            return;
        }
        for(int i=startIndex;i<nums.length;i++)
        {
            path.add(nums[i]);
            backtrack(nums,i+1);
            path.removeLast();
        }
    }
}

leetcode 90 子集II

题目描述

力扣题目链接(opens new window)

给定一个 可能包含重复元素 的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

思路解析

本题采用树层去重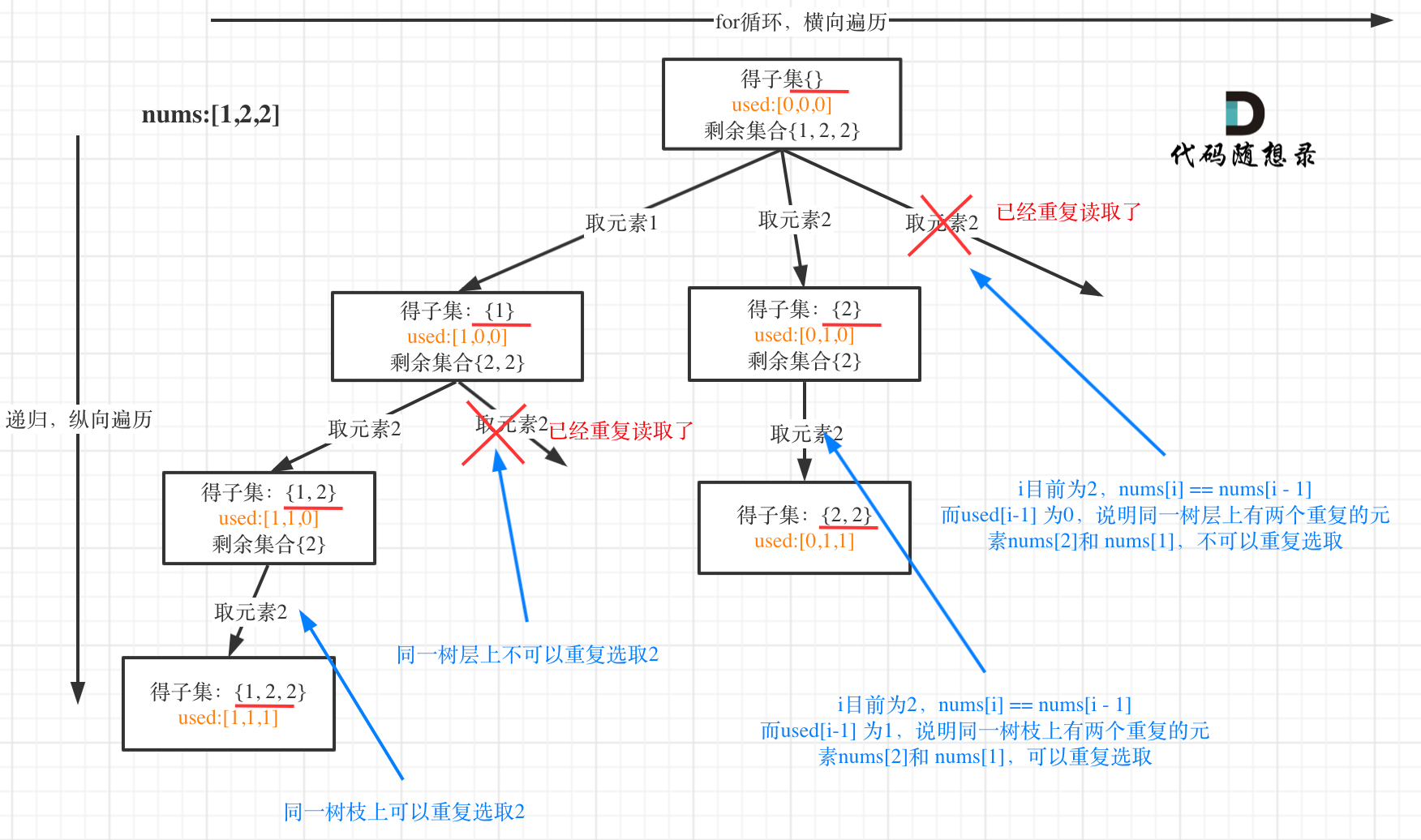 90.子集II

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


class Solution {
    List<List<Integer>>res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Boolean[]used=new Boolean[nums.length];
        Arrays.sort(nums);
        backtrack(nums,used,0);
        return res;
    }

    public void backtrack(int[]nums,Boolean[]used,int startIndex)
    {
        res.add(new ArrayList<>(path));
        if(startIndex>=nums.length)
            return;
        for(int i=startIndex;i<nums.length;i++)
        {
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false)
                continue;
            used[i]=true;
            path.add(nums[i]);
            backtrack(nums,used,i+1);
            used[i]=false;
            path.removeLast();
        }
    }
}

leetcode 491 递增子序列

题目描述

力扣题目链接(opens new window)

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

思路解析

本题不能使用used数组进行去重，因为不能对数组进行排序，因此使用set集合进行树层排序

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution {
    List<List<Integer>>res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtrack(nums,0);
        return res;
    }

    public void backtrack(int[]nums,int startIndex)
    {
        if(path.size()>=2)
        {
            res.add(new ArrayList<>(path));
        }
        HashSet<Integer>res=new HashSet<>();
        for(int i=startIndex;i<nums.length;i++)
        {
            if(!path.isEmpty()&&path.get(path.size()-1)>nums[i]||res.contains(nums[i]))
                continue;
            path.add(nums[i]);
            res.add(nums[i]);
            backtrack(nums,i+1);
            path.removeLast();
        }
    }
}

排列问题

统一解题模板

确定回溯函数模板返回值以及参数
1

void backtracking(boolean[]used,参数)
- 回溯算法中函数返回值一般为void。结果集合使用全局变量
- 回溯算法的参数中需要的boolean数组
确定回溯算法的终止条件
1 2 3 4

if (终止条件) { 存放结果; return; }
- 通常搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

确定单次遍历过程

1
2
3
4
5
6


for (int i=0;i<nums.length;i++) {
    判断是否被选择过
    处理节点;
    backtracking(used，其他参数); // 递归
    回溯，撤销处理结果
}

判断元素是否被选择，被选择后直接跳过
处理节点
- 将used[i]置为true
- 放入排列中
递归处理
回溯
- 将used[i]置为false
- 移除排列中

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


void backtracking(boolean[]used,参数){
	if (终止条件) {
    	存放结果;
    	return;
	}
	for (int i=0;i<nums.length;i++) {
    	if(used[i]==true)
            continue;
        处理节点;
        used[i]=true;
    	backtracking(used，其他参数); // 递归
        used[i]=false;
    	回溯，撤销处理结果
	}
}

leetcode 46 全排列

题目描述

力扣题目链接(opens new window)

给定一个 没有重复数字 的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路解析

参考解题模板

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


class Solution {
    List<List<Integer>> res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return res;
        }
        boolean[]used=new boolean[nums.length];
        backtrack(nums,used);
        return res;
    }

    public void backtrack(int[]nums,boolean[]used)
    {
        // 终止条件
        if(path.size()==nums.length)
        {
            res.add(new ArrayList<>(path));
            return;
        }
        // 单层遍历
        for(int i=0;i<nums.length;i++)
        {
            // 判断是否选择
            if(used[i]==true)
                continue;
            // 处理节点
            path.add(nums[i]);
            used[i]=true;
            backtrack(nums,used);
            // 回溯
            used[i]=false;
            path.removeLast();
        }
    }
}

leetcode 47 全排列II

题目描述

力扣题目链接(opens new window)

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

思路解析

本题需要树层去重，依然可以套用之前的做法。先对数组进行排序，然后利用 i>0&&nums[i-1]==nums[i]&&used[i-1]==false

进行树层去重

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


class Solution {
    List<List<Integer>>res=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);
        boolean[]used=new boolean[nums.length];
        backtrack(nums,used);
        return res;
    }

    public void backtrack(int[]nums,boolean[]used)
    {
        // 终止条件
        if(path.size()==nums.length)
        {
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0;i<nums.length;i++)
        {
            // 树层去重
            if(i>0&&nums[i-1]==nums[i]&&used[i-1]==false)
                continue;
            // 是否被选择
            if(used[i]==true)
                continue;
            // 处理节点
            path.add(nums[i]);
            used[i]=true;
            backtrack(nums,used);
            // 回溯
            path.removeLast();
            used[i]=false;
        }
    }
}

leetcode 332 重新安排行程

题目描述

力扣题目链接(opens new window)

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

提示：

如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
所有的机场都用三个大写字母表示（机场代码）。
假定所有机票至少存在一种合理的行程。
所有的机票必须都用一次且只能用一次。

示例 1：

输入：[[“MUC”, “LHR”], [“JFK”, “MUC”], [“SFO”, “SJC”], [“LHR”, “SFO”]]
输出：[“JFK”, “MUC”, “LHR”, “SFO”, “SJC”]

示例 2：

输入：[[“JFK”,“SFO”],[“JFK”,“ATL”],[“SFO”,“ATL”],[“ATL”,“JFK”],[“ATL”,“SFO”]]
输出：[“JFK”,“ATL”,“JFK”,“SFO”,“ATL”,“SFO”]
解释：另一种有效的行程是 [“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”]。但是它自然排序更大更靠后。

思路解析

本题的难点在于如何确定起点和重点的映射关系，同时还要按照字符的自然排序

可以考虑使用一个嵌套的map，键为起点，值为一个键是终点，值为航班次数的treeMap。

本题的目的是寻找一条符合条件的路径，不需要遍历完整个树，因此返回值为 boolean

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


class Solution {
    List<String>res=new LinkedList<>();
    Map<String,Map<String,Integer>>map=new HashMap<>();
    public List<String> findItinerary(List<List<String>> tickets) {
        // 建立映射关系(起点:(终点:航班次数))
        for(List<String>ticket:tickets)
        {
            // 获取起点和终点
            String src=ticket.get(0);
            String des=ticket.get(1);
            Map<String,Integer>temp;
            if(map.containsKey(src))
            {
                temp=map.get(src);
                temp.put(des,temp.getOrDefault(des,0)+1);
            }else{
                temp=new TreeMap<>();
                temp.put(des,1);
            }
            map.put(src,temp);
        }
        res.add("JFK");
        backtrack(tickets.size());
        return res;
    }

    public boolean backtrack(int ticketNum){
        // 终止条件
        if(res.size()==ticketNum+1)
        {
            return true;
        }
        // 获取队尾
        String last=res.getLast();
        // 查找以他为起点的航班情况
        Map<String,Integer>target=map.get(last);
        for(String t:target.keySet())
        {
            int count=target.get(t);
            if(count>0)
            {
                // 处理节点
                res.add(t);
                target.put(t,count-1);
                if(backtrack(ticketNum))
                    return true;
                res.remove(res.size()-1);
                target.put(t,count);
            }
        }
        return false;
    }

}

一维递归

leetcode 51 N皇后问题

题目描述

力扣题目链接(opens new window)

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

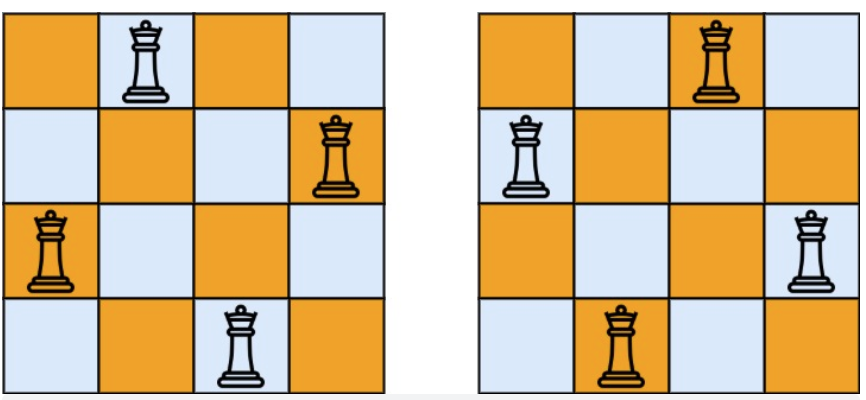
输入：n = 4
输出：[[".Q..","…Q",“Q…”,"..Q."],["..Q.",“Q…”,"…Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[[“Q”]]

思路解析

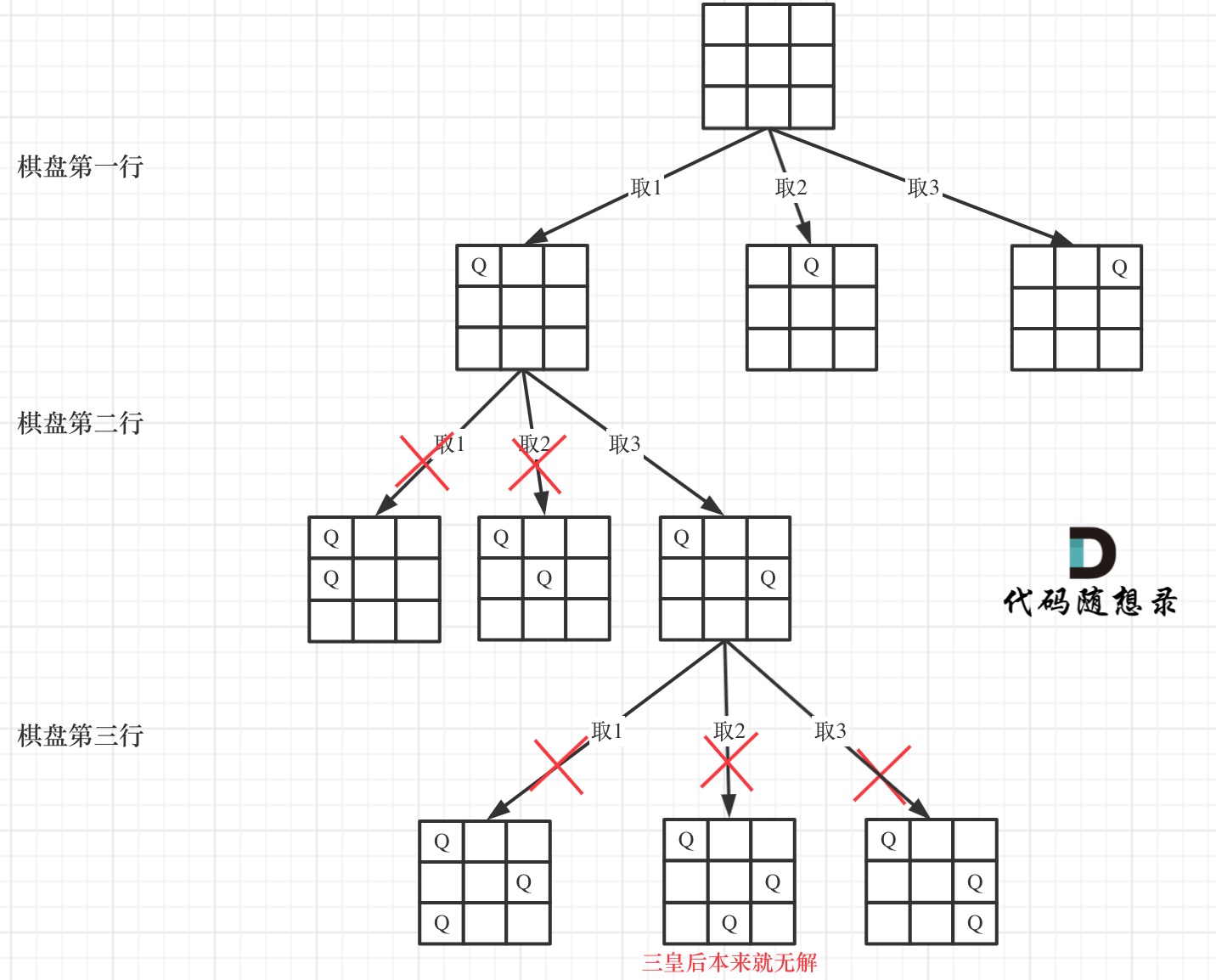
51.N皇后

递归函数参数
- 定义全局变量二维数组result来记录最终结果。
- 形参
  - 参数n是棋盘的大小，
  - row来记录当前遍历到棋盘的第几层了。
终止条件
- 遍历到最后一行停止
单层遍历
- 遍历每一列
  - 若放入皇后后棋盘合法则
    - 处理节点
    - 递归处理
    - 回溯

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67


class Solution {
    List<List<String>>res;
    public List<List<String>> solveNQueens(int n) {
        res=new ArrayList<>();
        char[][]chessboard=new char[n][n];
        for(char[] ch:chessboard)
        {
            Arrays.fill(ch,'.');
        }
        backtrack(n,0,chessboard);
        return res;
    }
    public void backtrack(int n,int row,char[][]chessboard)
    {
        // 终止条件
        if(row==n){
            res.add(ArrayToList(chessboard));
            return;
        }
        // 遍历每一列
        for(int col=0;col<n;col++)
        {
            // 判断是否合法
            if(isValid(row,col,n,chessboard))
            {
                chessboard[row][col]='Q';
                backtrack(n,row+1,chessboard);
                chessboard[row][col]='.';
            }
        }
    }
    // 检验假设放入皇后之后的棋盘是否合法
    public boolean isValid(int row,int col,int n,char[][]chessboard)
    {
        // 检验同一列
        for(int i=0;i<row;i++)
        {
            if(chessboard[i][col]=='Q')
                return false;
        }

        // 检验左上对角线
        for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        // 检验右上对角线
        for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
	
    // 将棋盘数字转换为List
    public List<String> ArrayToList(char[][]chessboard)
    {
        List<String>ans=new ArrayList<>();
        for(char[] ch:chessboard)
        {
            ans.add(new String(ch));
        }
        return ans;
    }
}

二维递归

题目描述

力扣题目链接(opens new window)

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则：数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。空白格用 ‘.’ 表示。

解数独

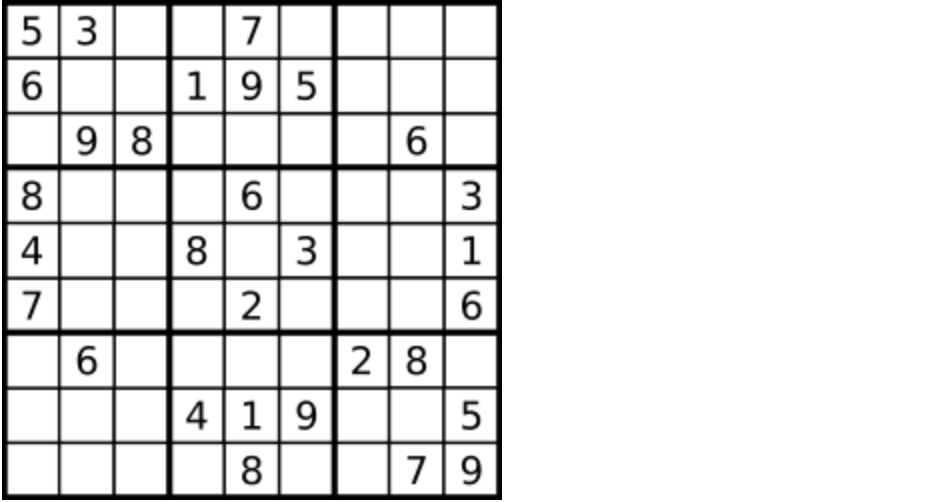
一个数独。

解数独

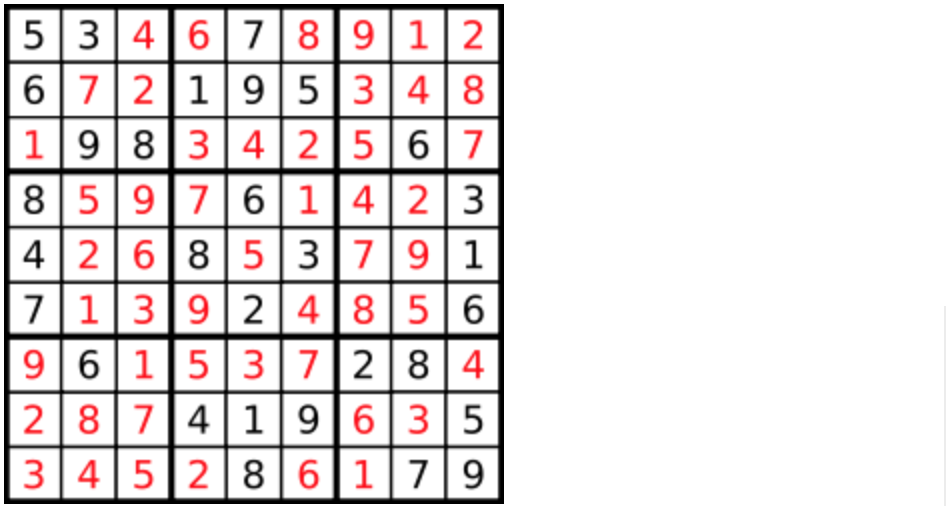
答案被标成红色。

提示：

给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

思路解析

相比于N皇后，数独问题需要在一个位置选择9个数字中的一个。同时在检验中如何保证数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次也是难点。对于保证数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。要向确定每个3x3 的起始行和起始列。

1
2


int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;

可以用来标识起始行和起始列

回溯函数的参数为boolean，因为本题只要找到一个符合的条件（就在树的叶子节点上）立刻就返回，相当于找从根节点到叶子节点一条唯一路径。

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


class Solution {
    public void solveSudoku(char[][] board) {
        backtrack(board);
    }

    public boolean backtrack(char[][]board)
    {
        // 确定每一个位置
        for(int i=0;i<9;i++)
        {
            for(int j=0;j<9;j++)
            {
                // 已经放入数组则跳过下面操作
                if(board[i][j]!='.')
                    continue;
                for(char k='1';k<='9';k++)
                {
                    if(isValid(i,j,k,board))
                    {
                        board[i][j]=k;
                        if(backtrack(board))
                            return true;
                        board[i][j]='.';
                    }
                }
                return false;
            }
        }
        return true;
    }

    // 检验放入数字前棋盘是否合法
    public boolean isValid(int row,int col,char val,char[][]board)
    {
        // 同行是否重复
        for (int i = 0; i < 9; i++){
            if (board[row][i] == val){
                return false;
            }
        }
        // 同列是否重复
        for (int j = 0; j < 9; j++){
            if (board[j][col] == val){
                return false;
            }
        }
        // 9宫格里是否重复
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++){
            for (int j = startCol; j < startCol + 3; j++){
                if (board[i][j] == val){
                    return false;
                }
            }
        }
        return true;
    }
}