数据结构与算法

树

课堂笔记转换

树的定义

树是是n（n≥0）结点的有限集合。n=0时，称为 空树 。任何一颗非空树只有一个根节点。

树具有以下特点：

  • 一棵树中的任意两个结点有且仅有唯一的一条路径连通。
  • 一棵树如果有 n 个结点，那么它一定恰好有 n-1 条边。
  • 一棵树不包含回路。

二叉树

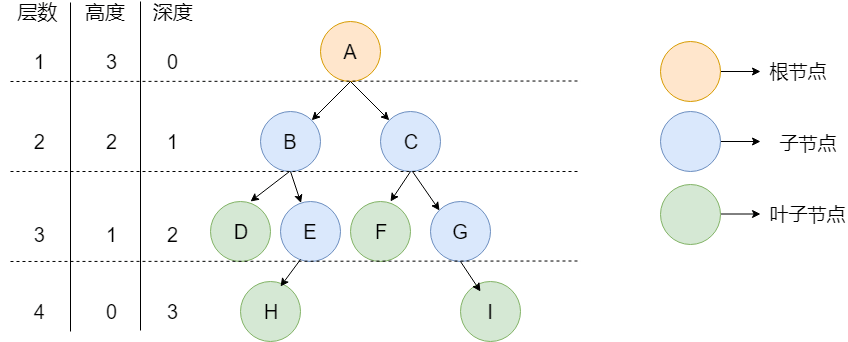
树的常见概念

节点相关

  • 节点 ：树中的每个元素都可以统称为节点。
  • 根节点 ：顶层节点或者说没有父节点的节点。
  • 父节点 ：若一个节点含有子节点，则这个节点称为其子节点的父节点。
  • 子节点 ：一个节点含有的子树的根节点称为该节点的子节点。
  • 兄弟节点 ：具有相同父节点的节点互称为兄弟节点。
  • 叶子节点：没有子节点的节点。

深度和高度

  • 节点的高度 ：该节点到叶子节点的最长路径所包含的边数
  • 节点的深度 ：根节点到该节点的路径所包含的边数，根节点的深度默认为0
  • 树的高度 ：树的高度等于根节点的高度，即根节点到叶子节点包含的边数
  • 树的深度 ：树的深度等于叶子节点的深度，即根节点到叶子节点包含的边数，所有树的深度等于树的高度

二叉树

定义

每个节点最多只有两个分支（即不存在分支度大于 2 的节点）的树结构

1
2
3
4
5
6
7
8

static class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    public TreeNode(int val){
        this.val=val;
    }
}

深度为k的二叉树的节点数为$[2^d,2^{d+1}-1]$

  • 最多节点（满二叉树）：$N=2^0+2^1+…2^d=2^{d+1}-1$
  • 最少节点（最后一层只有一个节点）：$N=2^0+2^1+..2^{d-1}+1=2^d$

分类

满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是 满二叉树 。也就是说，如果一个二叉树的层数为 K，且结点总数是$2^k -1 $，则它就是 满二叉树 。

满二叉树

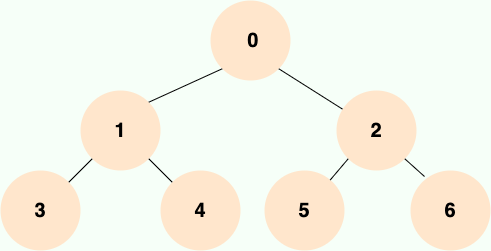
完全二叉树

除最后一层外，若其余层都是满的，并且最后一层是满的或者是在右边缺少连续若干节点，则这个二叉树就是 完全二叉树 。

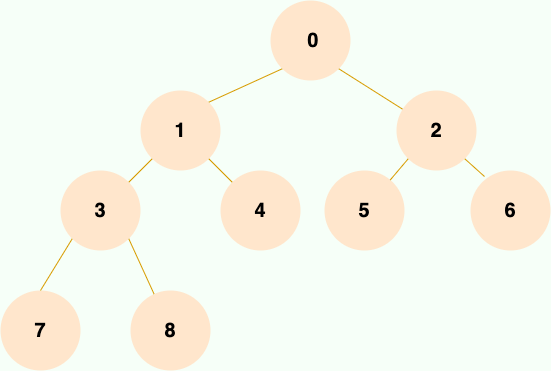
完全二叉树

二叉搜索树

对于每个节点X，它的左子树的所有项的值均小于X的元素值，右子树的所有项均大于X的元素值

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值

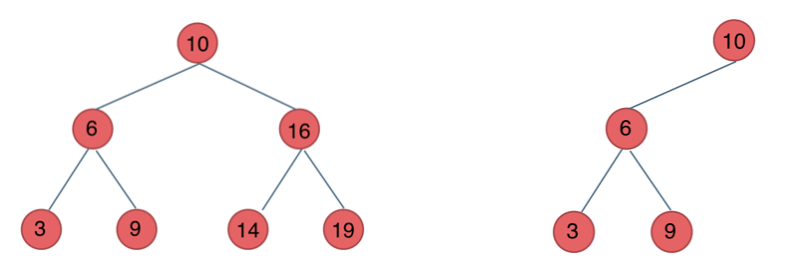
二叉搜索树

平衡二叉树

平衡二叉树 是一棵二叉搜索树，且具有以下性质：

  • 可以是一棵空树
  • 如果不是空树，它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

树的基本操作

遍历元素

前序遍历

二叉树的前序遍历，就是先输出根结点，再遍历左子树，最后遍历右子树，遍历左子树和右子树的时候，同样遵循先序遍历的规则。通常通过递归实现前序遍历。

1
2
3
4
5
6
7
8

public void preOrder(TreeNode root){
	if(root == null){
		return;
	}
	system.out.println(root.data);
	preOrder(root.left);
	preOrder(root.right);
}

中序遍历

二叉树的中序遍历，就是先递归中序遍历左子树，再输出根结点的值，再递归中序遍历右子树

1
2
3
4
5
6
7
8

public void inOrder(TreeNode root){
	if(root == null){
		return;
	}
	inOrder(root.left);
	system.out.println(root.data);
	inOrder(root.right);
}

后序遍历

二叉树的后序遍历，就是先递归后序遍历左子树，再递归后序遍历右子树，最后输出根结点的值

1
2
3
4
5
6
7
8

public void postOrder(TreeNode root){
	if(root == null){
		return;
	}
 	postOrder(root.left);
	postOrder(root.right);
	system.out.println(root.data);
}

层序遍历

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。通常使用队列实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

public void solver(TreeNode node) {
        if (node == null) return;
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(node);
        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);
                if (tmpNode.left != null) que.offer(tmpNode.left);
                if (tmpNode.right != null) que.offer(tmpNode.right);
                len--;
            }
            resList.add(itemList);
        }
    }

插入元素

通常插入元素的时间复杂度为$O(h)$

  • 对于二叉搜索树
    • 最坏情况：此时二叉搜索树退化为链表，时间复杂度为$O(n)$
    • 最好情况：此时二叉搜索树是平衡的，时间复杂度为$O(logn)$

因此可以通过二叉树的平衡操作来减少二叉树的深度

删除元素

删除节点有以下几种情况

  • 左右孩子都为空（叶子节点） ：直接删除节点， 返回NULL为根节点
  • 删除节点的左孩子为空，右孩子不为空 ：删除节点，右孩子补位，返回右孩子为根节点
  • 删除节点的右孩子为空，左孩子不为空 ：删除节点，左孩子补位，返回左孩子为根节点
  • 左右孩子节点都不为空 ：将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null)
            return null;
        if(root.val==key)
        {
            if(root.left==null)
                return root.right;
            else if(root.right==null)
                return root.left;
            else {
                TreeNode curr=root.right;
                while(curr.left!=null)
                    curr=curr.left;
                curr.left=root.left;
                root=root.right;
                return root;
            }
        }
        if(root.val>key)
            root.left=deleteNode(root.left,key);
        else
            root.right=deleteNode(root.right,key);
        return root;
    }

B树

定义

B 树是一种 自平衡的多路搜索树（multi-way search tree）

B树单一节点拥有的最多子节点数量，称为B树的 阶 。一个m阶的B树，树的节点具有以下特征

  • 子节点个数和元素个数

    • 根节点

      • 元素的个数：$[1,m-1]$
      • 子节点的个数：$[2,m]$

    • 中间节点

      • 元素个数：$[\lceil m/2 \rceil-1,m-1]$
      • 子节点的个数：$[\lceil m/2 \rceil,m]$

    • 每个节点的子节点个数和元素个数满足关系$子节点个数=元素个数+1$

  • 所有的叶子节点都位于同一层。

  • 每个节点中的元素从小到大排列，非叶子节点存储数据和索引

插入操作

  • 定位：找出插入该关键字的最低层中某个非叶结点（在B树中查找key时，会找到表示查找失败的叶节点，这样就确定了最底层非叶结点的插入位置。注意：插入位置一定是最底层中的某个非叶结点）。
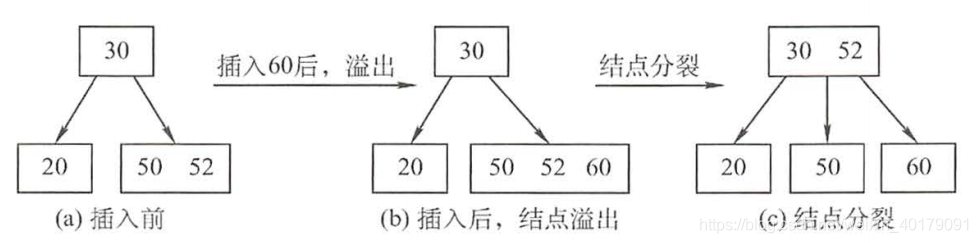
  • 插入。在B树中，每个非失败结点的关键字个数都在区间内。插入后的结点关键字个数小于m，可以直接插入；插入后检查被插入结点内关键字的个数，当插入后的结点关键字个数大于m-1时，必须对结点进行分裂。
  • 分裂的方法：取一个新结点，在插入key后的原结点，从中间位置$\lceil m/2 \rceil$将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放在新结点中，中间位置$\lceil m/2 \rceil$的结点插入原结点的父结点。若此时导致父结点的关键字个数也超过上限，则继续进行这种分裂操作，直至这个过程传到根节点为止，进而导致B树的高度增1。

分裂示例

删除操作

B树中的删除操作与插入操作类似，但是只需讨论删除终端结点（最底层非叶结点）中关键字的情形，因为当被删关键字k不在终端结点可以转换为在终端节点的情况

  • 直接删除：若被删除关键字所在结点的关键字个数$≥\lceil m/2 \rceil$，说明删除该关键字后仍满足B树的定义，则直接删去该关键字
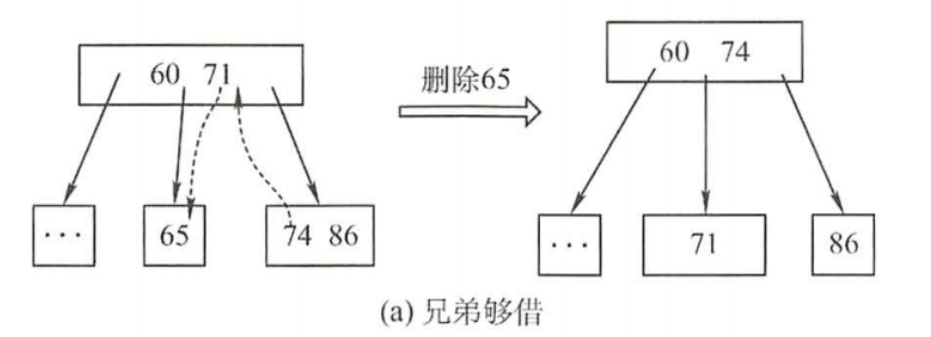
  • 兄弟够借：若被删除关键字在你所在结点删除前的关键字个数为$\lceil m/2 \rceil-1$，且与此结点相连的右（或左）兄弟结点的关键字个数$≥\lceil m/2 \rceil$，则需要调整该结点、右（或左）兄弟结点及其双亲结点父子交换，以达到新的平衡。兄弟够借
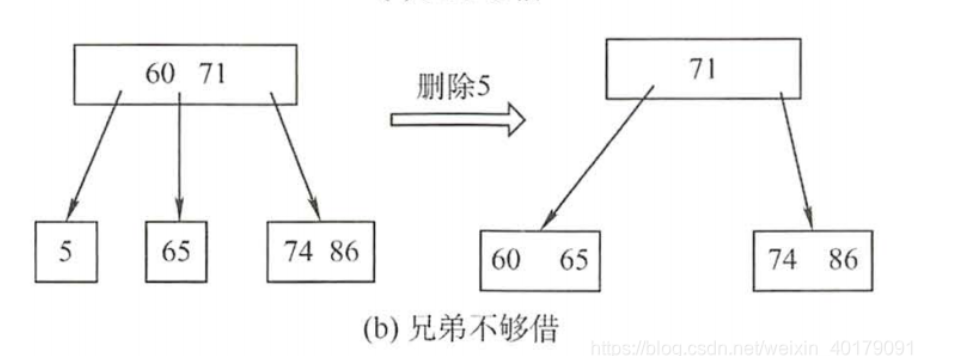
  • 兄弟不够借。若被删除关键字所在结点删除前的关键字个数为$\lceil m/2 \rceil-1$，且此时与该结点相邻的左、右兄弟结点的关键字个数均为$\lceil m/2 \rceil-1$，则将关键字删除后与左或者右兄弟结点进行合并兄弟不够借

B+树

定义

  • 每个分支结点最多有m棵子树（孩子结点）

  • 非叶根节点至少有两棵子树，其他每个分支结点至少有$\lceil m/2 \rceil$棵子树。

    • 在B+树中，每个结点（非根内部结点）的关键字个数n的范围$[\lceil m/2 \rceil,m]$；

      在B树中，每个结点（非根内部结点）的关键字个数n的范围是$[\lceil m/2 \rceil-1,m-1]$。

  • 结点的子树个数与关键字个数相等。

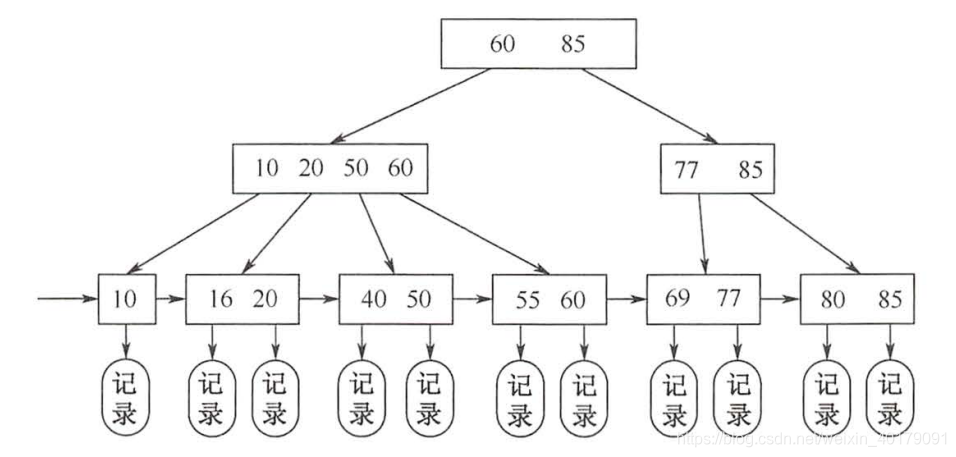
  • 所有叶结点包含全部关键字及指向对应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序互联链接起来。

  • 所有分支结点（可视为索引的索引）中仅仅包含它的各个子结点（即下一级的索引块）中关键字的最大值及指向子结点的指针。

B+树示例

堆

定义

堆的本质是一个二叉树。与二叉树的区别在于：对于这颗二叉树而言，任何一个子树 根节点上的数据和孩子节点上的数据之间是存在大小关系。

  • 大顶堆 ：根节点上的数据 大于或者等于 左右两个孩子
  • 小顶堆 ：根节点上的数据 小于或者等于 左右两个孩子

相关操作 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

		List<Integer>heap;
        MyHeap(){
            this.heap=new ArrayList<>();
        }
        MyHeap(ArrayList<Integer>heap){
            this.heap=heap;
        }
        public int getLeft(int index){
            return 2*index+1;
        }
        public int getRight(int index){
            return 2*index+2;
        }
        public int getParent(int index){
            return (index-1)/2;
        }
        public void swap(int left,int right){
            int temp=heap.get(right);
            heap.set(right,heap.get(left));
            heap.set(left,temp);
        }

插入操作

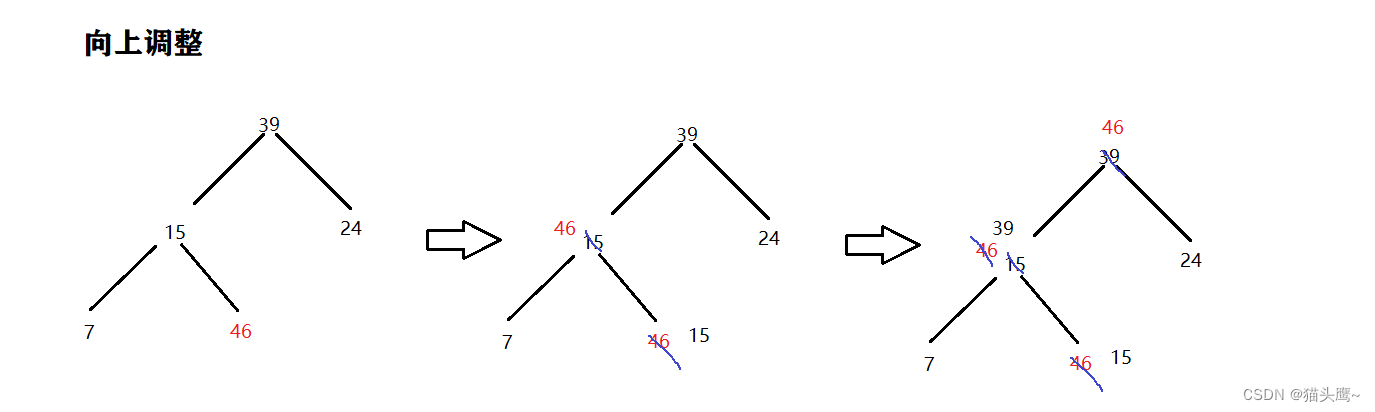
以大顶堆为例，需要对堆的叶子节点进行向上调整，使得堆符合定义。

  • 将元素插入到数组尾部中
  • 对数组尾部的元素进行向上调整
    • 比较插入节点和它的父亲节点，如果插入节点比其父亲节点大则交换位置
    • 继续迭代往上判断，直到 父节点比它大或者到达树的顶部

向上调整

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

	public void shiftUp(int index){
            while(index>0&&heap.get(index)>heap.get(getParent(index))){
                swap(index,getParent(index));
                index=getParent(index);
            }
        }
        public void push(int val){
            heap.add(val);
            shiftUp(heap.size()-1);
        }

删除操作

堆的删除只会删除堆顶的元素，因此需要对堆的根节点进行向下调整使得堆满足定义。对大顶堆来说

  • 将数组尾部的元素放入数组顶部并删除数组顶部
  • 对数组头部进行向下调整
    • 选取空穴的左右子节点中比较小的节点，与空穴进行交换
    • 继续迭代向下判断，直到空穴位于叶子节点
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

	public void shiftDown(int index,int heapSize){
            while(getLeft(index)<heapSize){
                int max=index;
                int left=getLeft(index);
                int right=getRight(index);
                if(left<heapSize&&heap.get(left)>heap.get(max)){
                    max=left;
                }
                if(right<heapSize&&heap.get(right)>heap.get(max)){
                    max=right;
                }
                if(max==index){
                    break;
                }
                swap(index,max);
                index=max;
            }
        }
        public int pop(){
            if(heap.isEmpty()){
                return Integer.MIN_VALUE;
            }
            int res=heap.get(0);
            int last=heap.remove(heap.size()-1);
            if(!heap.isEmpty()){
                heap.set(0,last);
                shiftDown(0,heap.size());
            }
            return res;
        }

建立堆

向下调整建立堆

时间复杂度为$O(nlogn)$

  • 找到最后一个父节点，将该父节点进行向下调整
  • 依次对所有的父节点进行向下调整
1
2
3
4
5
6

public void buildHeap(){
            int n=heap.size();
            for(int i=(n-2)/2;i>=0;i--){
                shiftDown(i,heap.size());
            }
        }

堆排序和Top K问题

升序使用大顶堆，降序使用小顶堆，时间复杂度为$O(nlogn)$

堆排序的过程如下（以升序排序为例）

  • 提取大顶堆的堆顶元素
  • 将当前最大的元素与末尾元素进行交换
  • 重新调整剩余元素形成新的堆
  • 循环往复直到堆中没有元素
1
2
3
4
5
6
7
8
9

	public void heapSort(){
            buildHeap();
            int size=heap.size();
            for(int i=heap.size()-1;i>=0;i--){
                swap(0,i);
                size--;
                shiftDown(0,size);
            }
        }

TOP K问题：比如说现在有10亿个数据，要选出其中最大的K个数，应该怎么选？

我们可以建一个容量为K的小根堆，然后先把前K个数据丢到堆里，之后依次遍历剩余的数据，将比堆顶大的数据代替堆顶进堆。

© 2022 - 2025 Tyritic
그 경기 끝나고 좀 멍하기 있었는데 여러분 이제 살면서 여러가
使用 Hugo 构建
主题 Stack 由 Jimmy 设计