数组旋转
leetcode 48 旋转数组
题目描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
1
2
|
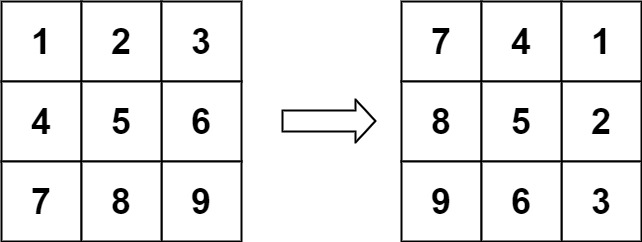
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
|
示例 2:
1
2
|
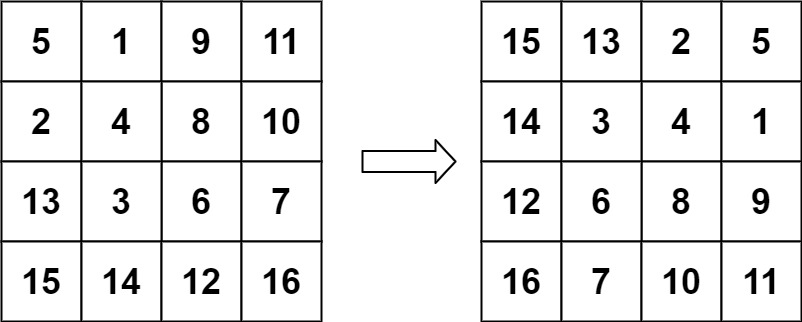
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
|
思路解析
对于矩阵中第i行的第j个元素,在旋转后,它出现在倒数第i列的第j个位置
因此对于矩阵中的元素 matrix[row][col] ,在旋转后,它的新位置为 matrix_new[col][n−row−1] 。
辅助数组法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
int[][] matrix_new = new int[n][n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
matrix_new[j][n - i - 1] = matrix[i][j];
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
matrix[i][j] = matrix_new[i][j];
}
}
}
}
|
翻转法
可以先将矩阵通过水平轴翻转,再通过主对角线翻转
$$
对于水平轴翻转而言,我们只需要枚举矩阵上半部分的元素,和下半部分的元素进行交换,即\\
matrix[row][col]\to^{水平轴翻转}matrix[n−row−1][col]
$$$$
对于主对角线翻转而言,我们只需要枚举对角线左侧的元素,和右侧的元素进行交换,即\\
matrix[row][col] \to^{主对角线翻转}matrix[col][row]
$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 水平翻转
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < n; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = temp;
}
}
// 主对角线翻转
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}
}
|
数学
位运算
-
逻辑左移:<< 末尾补0等价于乘2
-
逻辑右移:>>> 左端补0
-
算术右移:>> 左端最低位填充
-
按位求与:&
-
按位求或:|
-
按位异或: ^
- 归零律:任何数与自身异或等于0,即 X ⊕ X = 0。
- 恒等律:任何数与0异或等于其自身,即 X ⊕ 0 = X。
-
按位求非: ~
leetcode 338 比特位计数
题目描述
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
1
2
3
4
5
6
|
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
|
示例 2:
1
2
3
4
5
6
7
8
9
|
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
|
思路解析
将n与1进行与操作,等价于得到n的二进制位的最后一位,然后再让n右移一位
参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int[] countBits(int n) {
int[]res=new int[n+1];
for(int i=0;i<=n;i++)
{
res[i]=count(i);
}
return res;
}
public int count(int n)
{
int count=0;
while(n>0)
{
count+=n&1;
n>>=1;
}
return count;
}
}
|
模拟大数加法
leetcode 415 字符串相加
题目描述
题目链接
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
1
2
|
输入:num1 = "11", num2 = "123"
输出:"134"
|
示例 2:
1
2
|
输入:num1 = "456", num2 = "77"
输出:"533"
|
示例 3:
1
2
|
输入:num1 = "0", num2 = "0"
输出:"0"
|
思路解析
将相同数位对齐,从低到高逐位相加,如果当前位和超过 10,则向高位进一位。
定义两个指针 i 和 j 分别指向 num1和num2的末尾,即最低位,同时定义一个变量 add 维护当前是否有进位,然后从末尾到开头逐位相加即可。你可能会想两个数字位数不同怎么处理,这里我们统一在指针当前下标处于负数的时候返回 0,等价于对位数较短的数字进行了补零操作,这样就可以除去两个数字位数不同情况的处理
参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public String addStrings(String num1, String num2) {
StringBuilder ans=new StringBuilder();
int i=num1.length()-1;
int j=num2.length()-1;
int carry=0;
while(i>=0||j>=0){
int x=i>=0?num1.charAt(i)-'0':0;
int y=j>=0?num2.charAt(j)-'0':0;
int sum=x+y+carry;
ans.append(sum%10);
carry=sum/10;
i--;
j--;
}
if(carry==1){
ans.append(1);
}
return ans.reverse().toString();
}
}
|
数位运算
leetcode 7 整数反转
题目描述
题目链接
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
示例 2:
示例 3:
示例 4:
思路解析
- 设置res=0为结果
- 每次取数字的末尾数字temp
- 为了防止反转后溢出,当res大于整数的最大值/10或者整数的最小值/10则直接返回
- 将res乘以10+temp
参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public int reverse(int x) {
int res=0;
while(x!=0){
int temp=x%10;
if(res>Integer.MAX_VALUE/10||res<Integer.MIN_VALUE/10){
return 0;
}
res=res*10+temp;
x/=10;
}
return res;
}
}
|

