ZSet的定义

Redis的ZSet是一个可排序的set集合，与Java中的TreeSet有些类似，但底层数据结构却差别很大。ZSet中的每一个元素都带有一个score属性，可以基于score属性对元素排序，底层的实现是一个跳表（SkipList）加 hash表。ZSet具备下列特性：可排序元素不重复查询速度快

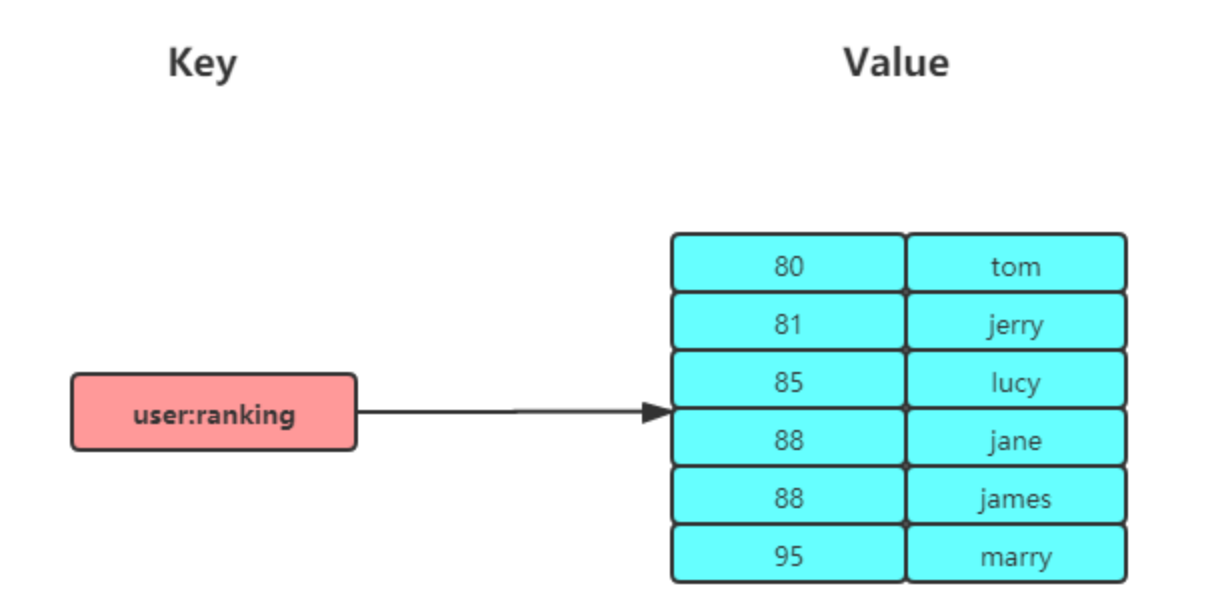
常用命令

• 查看
  • ZSCORE key member ：返回有序集合key中元素member的分值
  • ZCARD key ：返回有序集合key中元素个数
  • ZRANGE key start stop [WITHSCORES] ：正序获取有序集合key从start下标到stop下标的元素
  • ZRANGEBYSCORE key min max [WITHSCORES] [LIMIT offset count] ：返回有序集合中指定分数区间内的成员，分数由低到高排序。
  • ZCOUNT key min max ：计算有序集合中指定分数区间的成员数量。
• 加入元素
  • ZADD KEY_NAME SCORE1 VALUE1.. SCOREN VALUEN ：将一个或多个成员元素及其分数值加入到有序集当中
• 删除元素
  • ZREM key member [member ...] ：移除有序集中的一个或多个成员，不存在的成员将被忽略。

底层实现

Redis 中的 ZSet（有序集合，Sorted Set） 是一种由 跳表（Skip List） 和 哈希表（Hash Table） 组成的数据结构。ZSet 结合了集合（Set）的特性和排序功能，能够存储具有唯一性的成员，并根据成员的分数（score）进行排序。

ZSet 的实现由两个核心数据结构组成：

• 跳表（Skip List）：用于存储数据的排序和快速查找。
• 哈希表（Hash Table）：用于存储成员与其分数的映射，提供快速查找。

当 Zset 元素数量较少时，Redis 会使用压缩列表（Zip List）来节省内存

跳表的实现原理

跳表是在链表基础上改进过来的，实现了一种「多层」的有序链表

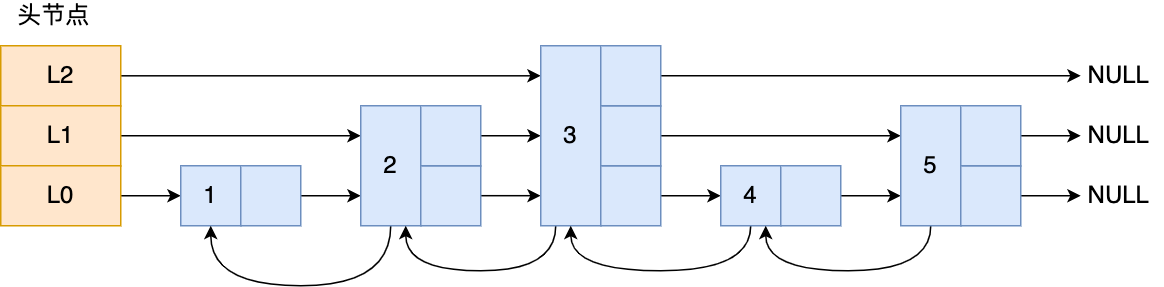
跳表的查找复杂度就是 $O(logN)$。

跳表是一个带有层级关系的链表，而且每一层级可以包含多个节点，每一个节点通过指针连接起来，实现这一特性就是靠跳表节点结构体中的 zskiplistLevel 结构体类型的 level 数组 。

数据结构

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

typedef struct zskiplistNode {
    //Zset 对象的元素值
    sds ele;
    //元素权重值
    double score;
    //后向指针
    struct zskiplistNode *backward;
  
    //节点的level数组，保存每层上的前向指针和跨度
    struct zskiplistLevel {
        struct zskiplistNode *forward; //每一层的前进指针
        unsigned long span;
    } level[];
} zskiplistNode;

• 对象的元素值ele

• 元素的权重值score

• 后向指针

• 层：跳跃表节点的 level 数组可以包含多个元素，每个元素都包含一个指向其它节点的指针，程序可以通过这些层来加快访问其它节点的速度，一般来说，层的数量越多，访问其它节点的速度就越快。每次创建一个新的跳跃表节点的时候，程序都根据幂次定律，随机生成一个介于 1 和 32 之间的值作为 level 数组的大小，这个大小就是层的“高度”

  • 前进指针：每个层都有一个指向表尾的前进指针（ level[i].forward 属性），用于从表头向表尾方向访问节点。
  • 跨度：用于记录两个节点之间的距离。跨度是用来计算排位（rank）的：在查找某个节点的过程中，将沿途访问过的所有层的跨度累计起来，得到的结果就是目标节点在跳跃表中的排位。

查找操作

从最高层开始，逐层向下，直到找到目标元素或确定元素不存在。查找效率高，时间复杂度为$ O(logn)$

跳表会从头节点的最高层开始，逐一遍历每一层。在遍历某一层的跳表节点时，会用跳表节点中的 SDS 类型的元素和元素的权重来进行判断，共有两个判断条件：

• 如果当前节点的权重小于要查找的权重时，跳表就会访问该层上的下一个节点。
• 如果当前节点的权重等于要查找的权重时，并且当前节点的 SDS 类型数据小于要查找的数据时，跳表就会访问该层上的下一个节点。

如果上面两个条件都不满足，或者下一个节点为空时，跳表就会使用目前遍历到的节点的 level 数组里的下一层指针，然后沿着下一层指针继续查找，这就相当于跳到了下一层接着查找。

插入操作

• 首先从最高层开始查找插入位置
• 随机决定新节点的层数
  • 跳表在创建节点时候，会生成范围为[0-1]的一个随机数，如果这个随机数小于 0.25（相当于概率 25%），那么层数就增加 1 层，然后继续生成下一个随机数，直到随机数的结果大于 0.25 结束，最终确定该节点的层数。
• 在相应的层中插入节点并更新指针。

示例

1
2
3
4
5

Level 4: 1  3  5  9  15
Level 3: 1  3  5  9
Level 2: 1  3  5  7  9
Level 1: 1  3  5  7  9  11  13
Level 0: 1  3  5  7  9  11  13  15

• 定位插入位置：需要定位新节点 8 应该插入的位置。我们从跳表的最高层开始，逐层向下查找。

  • 第 4 层

    • 从 1 -> 3 -> 5 -> 9 -> 15 开始。
    • 由于 8 小于 15 且大于 9，我们向下跳到第 3 层。

  • 第 3 层

    • 从 1 -> 3 -> 5 -> 9 开始。

    • 由于 8 小于 9 且大于 5，我们向下跳到第 2 层。

  • 第 2 层

    • 从 1 -> 3 -> 5 -> 7 -> 9 开始。

    • 由于 8 小于 9 且大于 7，我们向下跳到第 1 层。

  • 第 1 层

    • 从 1 -> 3 -> 5 -> 7 -> 9 -> 11 -> 13 开始。

    • 由于 8 小于 9 且大于 7，我们找到应该插入的位置，向下跳到第 0 层。

• 确定新节点的层数：随机确定新节点的层数。假设我们通过概率方法，决定新节点 8 将有 3 层（在最高的层数为 3 层）。

• 插入新节点

  • 第 0 层（最底层）
    • 在第 0 层，我们插入节点 8，保持有序性。8 位于 7 和 9 之间，因此我们将 7 的指针指向 8，8 的指针指向 9，然后更新链表。更新后的第 0 层指针：1 -> 3 -> 5 -> 7 -> 8 -> 9 -> 11 -> 13 -> 15
  • 第 1 层
    • 在第 1 层，我们插入节点 8，8 位于 7 和 9 之间。我们将 7 的指针指向 8，8 的指针指向 9，更新链表。更新后的第 1 层指针1 -> 3 -> 5 -> 7 -> 8 -> 9 -> 11 -> 13
  • 第 2 层
    • 在第 2 层，我们插入节点 8，8 位于 7 和 9 之间。我们将 7 的指针指向 8，8 的指针指向 9，更新链表。更新后的第 2 层指针：1 -> 3 -> 5 -> 7 -> 8 -> 9
  • 第 3 层
    • 在第 3 层，我们插入节点 8，8 位于 7 和 9 之间。我们将 7 的指针指向 8，8 的指针指向 9，更新链表。更新后的第 3 层指针：1 -> 3 -> 5 -> 7 -> 8 -> 9

• 最终跳表结构

  插入节点 8 后，跳表的结构应该如下所示：

  1 2 3 4 5

  Level 4: 1 3 5 7 8 9 15 Level 3: 1 3 5 7 8 9 Level 2: 1 3 5 7 8 9 Level 1: 1 3 5 7 8 9 11 13 Level 0: 1 3 5 7 8 9 11 13 15

删除操作

• 查找删除操作
• 对于每一层，检查该层是否存在待删除的节点。如果该节点存在，则需要更新该层中前后节点的指针，将它们连接起来。
• 继续往下处理，直到删除节点的层次遍历完毕。

示例

1
2
3
4
5

Level 4: 1  3  5  9  15
Level 3: 1  3  5  9
Level 2: 1  3  5  7  9
Level 1: 1  3  5  7  9  11  13
Level 0: 1  3  5  7  9  11  13  15

• 定位节点：需要找到节点 9 在各层的位置。假设我们从最高层开始：

  • 在第 4 层（最上层），节点 9 存在。
  • 在第 3 层，节点 9 存在。
  • 在第 2 层，节点 9 存在。
  • 在第 1 层，节点 9 存在。
  • 在第 0 层（底层），节点 9 存在。

• 删除节点并更新指针：从最高层开始删除节点 9，并逐层更新指针。

  • 删除第 4 层的节点 9

    • 在第 4 层，节点 9的前驱是 5，后继是 15。我们需要将 5 的指针指向 15，即跳过 9。
    • 更新后的第 4 层指针：1 -> 3 -> 5 -> 15。

  • 删除第 3 层的节点 9

    • 在第 3 层，节点 9的前驱是 5，后继是 None。我们需要将 5 的指针指向 None。

    • 更新后的第 3 层指针：1 -> 3 -> 5。

  • 删除第 2 层的节点 9

  • 在第 2 层，节点 9的前驱是 7，后继是 None。我们需要将 7 的指针指向 None。

  • 更新后的第 2 层指针：1 -> 3 -> 5 -> 7。

  • 删除第 1 层的节点 9

    • 在第 1 层，节点 9的前驱是 7，后继是 11。我们需要将 7 的指针指向 11，即跳过 9。

    • 更新后的第 1 层指针：1 -> 3 -> 5 -> 7 -> 11 -> 13。

  • 删除第 0 层的节点 9

    • 在第 0 层（最底层），节点 9的前驱是 7，后继是 11。我们需要将 7 的指针指向 11，即跳过 9。

    • 更新后的第 0 层指针：1 -> 3 -> 5 -> 7 -> 11 -> 13 -> 15。

跳表和B+树的区别

Redis 是内存数据库，跳表在实现简单性、写入性能、内存访问模式等方面的综合优势，使其成为更合适的选择。

Redis 选择使用跳表（Skip List）而不是 B+ 树来实现有序集合（Sorted Set）等数据结构，是经过多方面权衡后的结果。

• 内存结构和访问模式差异

  • B+ 树的特性
    • 磁盘友好 ：B+ 树的设计目标是优化磁盘I/O，通过减少树的高度来降低磁盘寻道次数（例如，一个3层的B+树可以管理数百万数据）。
    • 节点填充率高 ：每个节点存储多个键值（Page/Block），适合批量读写。
    • 范围查询高效 ：叶子节点形成有序链表，范围查询（如 ZRANGE）性能极佳。
  • 跳表的特性
    • 内存友好 ：跳表基于链表，通过多级索引加速查询，内存访问模式更符合CPU缓存局部性（指针跳跃更少）。
    • 简单灵活 ：插入/删除时仅需调整局部指针，无需复杂的节点分裂与合并。
    • 概率平衡 ：通过随机层高实现近似平衡，避免了严格的平衡约束（如红黑树的旋转）。

• 实现复杂度

  • B+ 树的实现复杂度：

    • 节点分裂与合并 ：插入/删除时可能触发节点分裂或合并，需要复杂的再平衡逻辑。
    • 锁竞争 ：在并发环境下，B+ 树的锁粒度较粗（如页锁），容易成为性能瓶颈。

  • 跳表的实现复杂度：

    • 无再平衡操作 ：插入时只需随机生成层高，删除时直接移除节点并调整指针。

    • 细粒度锁或无锁 ：跳表可以通过分段锁或无锁结构（如 CAS）实现高效并发。

常见应用

实现延时队列

• 任务添加到 zset 中，score 为任务的执行时间戳，value 为任务的内容。
• 定期（例如每秒）从 zset 中获取 score 小于当前时间戳的任务，然后执行任务。
• 任务执行后，从 zset 中删除任务。